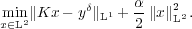
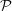 )
)
For non-Gaussian noise models such as impulsive noise, L1 data fitting is more appropriate than standard L2 terms, but leads to non-differentiable functionals to be minimized. The goal is to develop superlinearly convergent numerical methods for such inverse problems, including the automatic choice of regularization parameters.
Noise models of impulse type, e.g. salt-and-pepper or random-valued noise, arise in measurements because of malfunctioning pixels in camera sensors, faulty memory locations in hardware, or transmission in noisy channels. The advantage of using the L1 norm is given by the fact that the solution is more robust with respect to outliers when compared to the L2 norm.
We consider for a bounded linear operator K :L2 → L2, noisy data yδ ∈ L2(Ω) and α > 0 the minimization problem
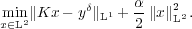 | (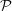 ) ) |
Using Fenchel duality, the dual problem is found to be
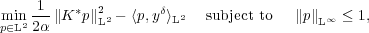
Introducing a Moreau-Yosida approximation of the box constraints and a smoothing term, this problem can be solved using a superlinearly convergent semi-smooth Newton method: Given pk, find pk+1 satisfying
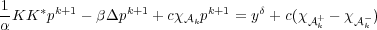
where χ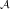 k+ = {x : pk(x) > 1},χ
k+ = {x : pk(x) > 1},χ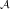 k- = {x : pk(x) < -1} denote the active sets, c > 0 is the penalty parameter for the
Moreau-Yosida approximation and β > 0 is the smoothing parameter to ensure semi-smoothness. It can be shown
that the dual solution pα acts as a noise indicator. The solution of the primal problem (
k- = {x : pk(x) < -1} denote the active sets, c > 0 is the penalty parameter for the
Moreau-Yosida approximation and β > 0 is the smoothing parameter to ensure semi-smoothness. It can be shown
that the dual solution pα acts as a noise indicator. The solution of the primal problem (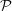 ) is then given by
xα =
) is then given by
xα = 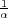 K*p
α.
K*p
α.
The parameter choice method for α is based on a balancing principle: Fix σ > 1 and find α such that
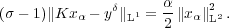
The balancing parameter α* can be calculated by a fixed point iteration using a model function, which is a
rational interpolant of the value F(α) = ∥Kxα - yδ∥L1 + 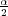 ∥xα∥L22 and its derivative F′(α) =
∥xα∥L22 and its derivative F′(α) = 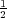 ∥xα∥L22 at the
iterates.
∥xα∥L22 at the
iterates.
Inverse source problem for the Laplace operator (i.e., K = (-Δ)-1), 30% of data corrupted by random-valued noise:
 |
 |
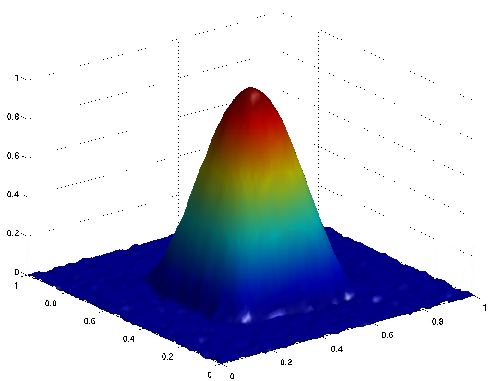 |
| (a) exact solution
|
(b) noisy data
|
(c) reconstruction
|
Reference: A semismooth Newton method for L1 data fitting with automatic choice of regularization parameters and noise calibration, submitted (preprint and Matlab code)