 :
:
Optimal control problems for partial differential equations with controls in the space L1 are in general not well-posed, since boundedness in L1 is not sufficient for the existence of a weakly converging subsequence. The natural functional-analytic framework for such problems is the space of bounded Borel measures. The goal is to develop efficient numerical methods for the solution of optimal control problems with measures.
L1-type penalties are relevant in settings where the cost of the control is a linear function of its magnitude (e.g., fuel consumption when the control is motor thrust). Also, L1-type costs are known to lead to sparse controls, which motivates using this approach for the optimal placement of discrete sensors or actuators.
Since the space of functions of bounded variation (BV) can be taken as the space of functions in L1 for which the distributional gradient is a measure, this setting also extends to optimal control problems with total variation costs, which are known to favor piecewise constant controls.
Let A be a second order differential operator, z ∈ L2 and α > 0 be given. We consider the following optimal control
problem in the space of bounded Borel measures 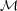 :
:
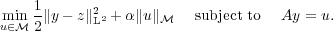 | (1) |
Using Fenchel duality, we find the predual problem, which is posed in 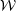 := H2 ∩ H01:
:= H2 ∩ H01:
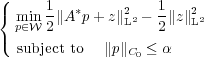 |
Introducing a Moreau-Yosida approximation of the box constraints, this problem can be solved using a superlinearly convergent semi-smooth Newton method: Given pk, find pk+1 satisfying
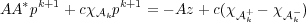
where χ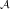 k+ = {x : pk(x) > α},χ
k+ = {x : pk(x) > α},χ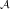 k- = {x : pk(x) < -α} denote the active sets and c > 0 is the penalty parameter for the
Moreau-Yosida approximation. The solution of the primal problem (1) is then given by u* = AA*p* + Az.
k- = {x : pk(x) < -α} denote the active sets and c > 0 is the penalty parameter for the
Moreau-Yosida approximation. The solution of the primal problem (1) is then given by u* = AA*p* + Az.
 |
 |
 |
|
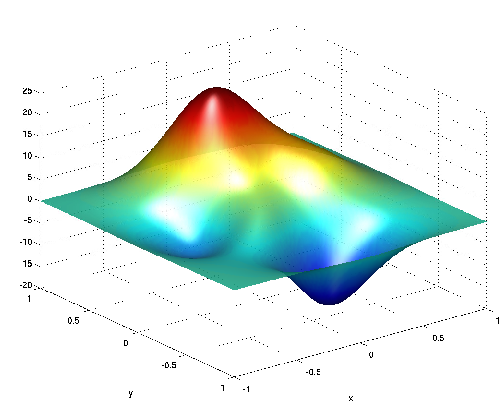
(a) Optimal control u*∈ L2 (α = 10-2)
|
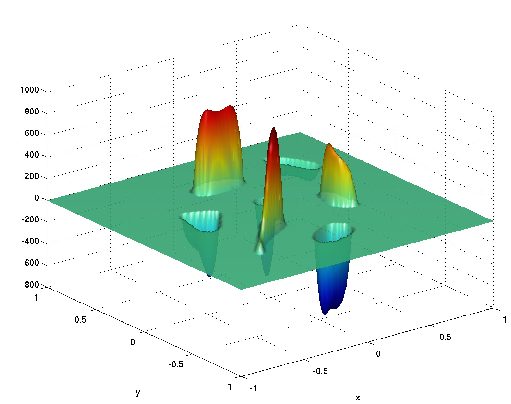
(b) Optimal control u*∈ 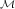 (α = 10-2) (α = 10-2) |
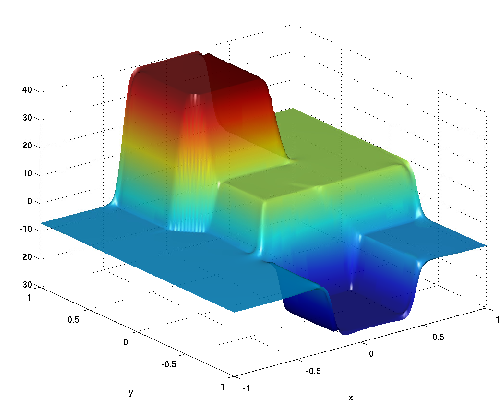
(c) Optimal control u*∈ BV (α = 10-2) |
Reference: A duality-based approach to elliptic control problems in non-reflexive Banach spaces, to appear in ESAIM: Control, Optimisation and Calculus of Variations (preprint: http://www.uni-graz.at/~clason/preprints/EllipticControlBanach.pdf)